A. Definisi
Lingkaran adalah kedudukan titik-titik yang berjarak sama (r) terhadap sebuah titik tertentu (Misalkan titik 0). Sebuah titik tertentu adalah pusat lingkaran (Titik 0 disebut titik pusat dan r disebut jari-jari (radius)).
B. Persamaan Lingkaran
- Persamaan lingkaran dengan pusat (0,0) dan jari-jari = r.

x2 + y2 = r2 - Persamaan lingkaran dengan pusat (a,b) dan jari-jari = r.
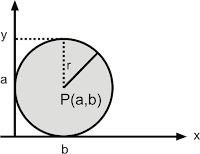
(x - a)2 + (y - a)2 = r2 - Bentuk umum persamaan lingkaran
x2 + y2 + 2ax + 2by + c = 0
Syarat :
koefisien x2 + y2 harus sama dan tidak sama dengan nol.
Persamaan tersebut mempunyai :
- Pusat (P) = (-a, -b)
- Jari-jari(r) = √(-a)2 + (-b)2 - c
C. Posisi titik terhadap lingkaran
Diketahui sebuah lingkaran dengan persamaan
L : x2 + y2 + 2ax + 2by + c = 0 dan sebuah titik A(x,y).
kedudukan titik A(x1, y2) terhadap lingkaran L adalah :
Kp : x12 + y12 + 2ax1 + 2by1 + c = 0
Keterangan :
A(x1, y2) berada di luar lingkaran.L : x2 + y2 + 2ax + 2by + c = 0 dan sebuah titik A(x,y).
kedudukan titik A(x1, y2) terhadap lingkaran L adalah :
Kp : x12 + y12 + 2ax1 + 2by1 + c = 0
Keterangan :
- Jika Kp > 0 maka titik A(x1, y2) berada di luar lingkaran
- Kp < 0 maka titik A(x1, y2) berada di dalam lingkaran
- Kp = 0 maka titik A(x1, y2) berada pada lingkaran
Jika dibuat garis singgung pada lingkaran yang melalui A(x1, y2) maka jarak dari titik A(x1, y2) ketitik singgungan adalah d = √Kp dengan
D. Hubungan Garis dengan Lingkaran
Diberikan garis g : y= mx + n dengan lngkaran L ≡ x2 + y2 = r2 hubungan antara garis g dengan lingkaran L dapat diselidiki dengan cara mensubtitusikan garis g ke L.L ≡ x2 + y2 = r2 dan g ≡ y = mx + n
L ≡ x2 + (mx + n)2 - r2 = 0
L ≡ x2 + m2x2 + 2mnx + n2 - r2 = 0
L ≡ (1 + m2)x2 + 2mnx + n2 - r2 = 0
L ≡ x2 + (mx + n)2 - r2 = 0
L ≡ x2 + m2x2 + 2mnx + n2 - r2 = 0
L ≡ (1 + m2)x2 + 2mnx + n2 - r2 = 0
Persamaan di atas merupakan persamaan kuadrat dengan diskriminan :
D = 4m2r2 - 4n2 + 4r2
Selanjutnya, ada 3 kemungkinan yang terjadi, yaitu :
(1) D > 0 maka garis memotong lingkaran pada dua titik.
(2) D = 0 maka garis memotong lingkaran pada satu titik (garis menyinggung lingkaran).
(3) D < 0 maka garis tidak menyinggung lingkaran.
E. Persamaan Garis Singgung Lingkaran
Ada berberapa cara untuk menentukannya :
- Persamaan Garis Singgung di Titik P(x1, y2)
x2 + y2 + Ax + Bx + C
 Persamaan Garis G :
Persamaan Garis G :
(y - y1)=m2(x - x1)
Jari - jari ⊥ garis g, artinya m1.m2 = -1 sehingga diperoleh :
m1 = y1 - ypx1 - xp
- Persamaan Garis Singgung pada Lingkaran x2 + y2 = r2 di titik (x1, y2)
Rumus :
x1x + y1y = r2 - Persamaan Garis Singgung di titik P(x1, y2) pada Lingkaran :
x2 + y2 + 2ax + 2by + c = 0
Rumus :
x1x + y1y + a(x1 + x) + b(y1 + y) + c = 0 - Persamaan Garis Singgung dengan gradien m pada Lingkaran yang berpusat di titik O(0,0) dengan jari-jari r.
Rumus :
y = mx ± r √1 + m2 - Persamaan Garis Singgung dengan gradien m pada Lingkaran : (x - a)2 + (y - b)2 = r2
Rumus :
y - b = m(x - a) ± r √1 + m2
Menentukan Jari - jari (r).

Jari-jari (r) :
Ax1 + By1 + C√A2 + B2


0 Response to "Lingkaran"
Post a Comment