Transformasi

Bahan Stempel Harga Murah, Jelas, Lengkap, Recommended di walisongo.co.id

Transformasi Geometri adalah suatu fungsi yang mengaitkan antara titik di suatu bidang dengan aturan tertentu. Pengaitan ini dapat dipandang secara aljabar atau geometri.

A. Translasi

Contoh Translasi dalam kehidupan sehari-hari adalah pergeseran atau perpindahan orang pada eskalator dan lift. Peralatan yang biasa di pakai mal untuk memindahkan orang dari satu lantai ke lantai lain.

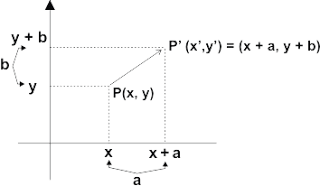Translasi (Pergeseran)

Translasi (T) = (a/b) memetakan titik P(x, y) ke titik P'(x', y')
maka x' = x + a dan y' = y + b, atau P'(x + a, x + b).

Dapat di tuliskan dalam bentuk :

A(x, y) ---> A'(x + a, x + b)

B. Refleksi

Suatu transformasi yang memasangkan setiap titik pada bidang rotasi atau proses memutar bangun geometri terhadap titik yang dinamakan titik pusat.

1. Pencerminan terhadap Garis x = a dan y = b
   

   

   
   

   • Pencerminan terhadap garis x = a menghasilkan bayangan P'(2a-x, y)
     

     x' y'

     =

     2a - x y

     
     Matriks Transformasinya
     

     x' y'

     =

     -1 0 0 1

     x - a y

     +

     a b

   • Pencerminan terhadap garis y = b menghasilkan bayangan P'(x, 2b-y)
     

     x' y'

     =

     x 2b - y

     
     Matriks Transformasinya
     

     x' y'

     =

     1 0 0 -1

     x y - b

     +

     a b

   • Pencerminan terhadap garis x = a dan y = b menghasilkan bayangan P'(2a-x, 2b-y)
     

     x' y'

     =

     2a - x 2b - y

     
     
2. Perceminan Terhadap Sumbu X, Sumbu Y, Garis y = x, dan y = -x
• Pencerminan terhadap sumbu x menghasilkan bayangan P'(x, -y)
  

  x' y'

  =

  x -y

  
  Matriks Transformasinya
  

  x' y'

  =

  1 0 0 -1

  x y

  
  
• Pencerminan terhadap sumbu y menghasilkan bayangan P'(-x, y)
  

  x' y'

  =

  -x y

  
  Matriks Transformasinya
  

  x' y'

  =

  -1 0 0 1

  x y

  
  
• Pencerminan terhadap sumbu y = x menghasilkan bayangan P'(y, x)
  

  x' y'

  =

  x y

  
  Matriks Transformasinya
  

  x' y'

  =

  0 1 1 0

  x y

  
  
• Pencerminan terhadap sumbu y = -x menghasilkan bayangan P'(-y, -x)
  

  x' y'

  =

  -x -y

  
  Matriks Transformasinya
  

  x' y'

  =

  0 -1 -1 0

  x y

  
  
3. Perceminan Terhadap Garis y = mx dan y = mx + c saat m = tan α
   
   • Pencerminan terhadap garis y = mx saat m = tan α menghasilkan bayangan
     P'(x cos2α + y sin2α, x sin2α - y cos2α)
     

     x' y'

     =

     x cos2α + y sin2α x sin2α - y cos2α

     Matriks Transformasinya
     

     x' y'

     =

     cos2α sin2α sin2α -cos2α

     x y

   • Perceminan Terhadap Garis y = mx + c saat m = tan α menghasilkan bayangan
     P'(x cos2α + (y-c)sin2α, x sin2α - (y-c)cos2α + c)
     

     x' y'

     =

     x cos2α + (y-c)sin2α x sin2α - (y-c)cos2α + c)

     Matriks Transformasinya
     

     x' y'

     =

     cos2α sin2α sin2α -cos2α

     x y - c

     +

     0 c

C. Rotasi (Pemutaran)

Rotasi ditentukan oleh arah rotasi dan besar sudut rotasi dengan sifat bayangan cermin dari titik-titik yang telah dipindahkan.

1. Rotasi terhadap titik pusat O(0,0) menghasilkan bayangan
   P'(x cos α - y sin α, x sin α + y cos α)
   

   x' y'

   =

   x cos α - y sin α x sin α + y cos α

   
   Matriks Transformasinya
   

   x' y'

   =

   cos α -sin α sin α cos α

   x y

   
   
2. Rotasi terhadap titik pusat P(a, b) menghasilkan bayangan
   P'(x cos α - y sin α, x sin α + y vos α)
   

   x' y'

   =

   x cos α - y sin α x sin α + y vos α

   
   Matriks Transformasinya
   

   x' y'

   =

   cos α -sin α sin α cos α

   x - a y - b

   +

   a b

   
   

D. Dilatasi (Perkalian)

Dilatasi adalah transformasi yang mengubah ukuran atau skala suatu bangun geometri (pembesaran/pengecilan), tetapi tidak mengubah bentuk dari bangun tersebut

1. Dilatasi [0,k]
   Matriks Transformasinya
   

   x' y'

   =

   k 0 0 k

   x y

   
   
2. Dilatasi [P(a,b),k]
   Matriks Transformasinya
   

   x' y'

   =

   k 0 0 k

   x - a y - b

   x y

   +

   a b

Posted by Adam Prasetya