Himpunan

Bahan Stempel Harga Murah, Jelas, Lengkap, Recommended di walisongo.co.id

A. Himpunan

Himpunan adalah kumpulan objek atau unsur yang di definiskan dengan jelas.

• ∈ artinya anggota himpunan. a ∈ A, artinya a anggota himpunan A.
• ∉ artinya bukan anggota himpunan.
• Banyak nya anggota himpunan A di notasikan dengan n(A)
• Penulisan anggota himpunan di dalam "{ }".
• Apabila bilangan tidak bisa di tuliskan satu persatu maka dapat di tulis dengan tiga titik " ... ".

Dalam Matematika, kamu harus tahu : 

• Bilangan Asli, terdiri dari bilangan-bilangan 1, 2, 3, 4, ...
• Bilangan Cacah, terdiri dari bilangan-bilangan 0, 1, 2, 3, 4 ...
• Bilangan Prima, terdiri dari bilangan-bilangan 2, ,3, 5, 7 ...
• Bilangan Bulat, terdiri dari bilangan-bilangan 1, -1, 2, -2, 3 ...

Contoh :

• Dari Bilangan di atas kita bisa membentuk sebuah himpunan.
  A = { 1, 2, 3, 4, ... }
  C = { 0, 1, 2, 3, 4 ... }
  P = { 2, ,3, 5, 7 ... }
  B = { 1, -1, 2, -2, 3 ... }
• Himpunan A = { Adam, Bima, Rian, Nico, Surya }
  Adam memiliki adik bernama Desi.
  maka Adam ∈ A (Adam anggota dari himpunan A) dan Desi ∉ A (Desi bukan anggota dari himpunan A).

1. Himpunan Berhingga dan Tak Berhingga
   
• Himpunan Berhingga
  Misalnya :
  K = { 2, 5, 8, 9, 5, 4, 2, 3 }, A = { Wati, Havez, Dava, Marco, Leo }.
  Himpunan K & A adalah himpunan berhingga.
• Himpunan Tak Berhingga
  Misalnya :
  K = { 1, 2, 3, 4, 5, 6, ... }, P = { ..., 1, 2, 3, 4, 5 }
  Himpunan K & P adalah himpunan tak berhingga.
2. Himpunan Kosong, Nol, dan Himpunan Semesta
   
   • Himpunan Kosong
     Himpunan yang tidak memiliki anggota, di tuliskan "{}" atau "∅".
     Contoh :
     Himpunan nama bulan yang terdiri dari 32 hari.
   • Himpunan Nol
     Himpunan yang hanya memiliki 0 sebagai anggota nya.
     Contoh :
     Himpunan bilangan bulat antara -1 dan 1
   • Himpunan Semesta
     Himpunan yang memuat semua anggota himpunan yang sedang dibicarakan. lambangnya adalah S
     Contoh :
     Himpunan A = { Mangga, Jeruk, Apel, Semangka, Nanas }.
     Himpunan Semestanya adalah S = { Buah - buahan }

B. Diagram Venn

Misalnya himpunan A = { 1, 3, 5, 7, 9 } maka himpunan Semestanya S = { 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 }. maka di Diagram Venn nya adalah

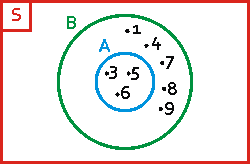
• Himpunan Semesta di lambangkan dengan S dan di letakan di pojok kiri atas.
• Setiap himpunan harus memiliki batas sendiri atau kurva tertutup. Seperti himpunan A dengan anggota di dalam lingkaran.
• Setiap anggota himpunan di beri tanda titik dan di beri nama.

C. Himpunan Bagian

Misalnya, himpunan A = { 3, 5, 6 } dan B = { 1,  3, 4, 5, 8, 6, 7, 9 }. anggota A merupakan bagian dari anggota B, maka A adalah himpunan bagian dari B atau A ⊂ B atau B ⊃ A.

Diagram Venn nya adalah :

Banyaknya himpunan bagian dari dari suatu himpunan adalah "2ⁿ dengan n adalah banyak anggota himpunan"
Contoh :

1. A = { 2, 3, 1, 6 }
   n(A) = 4 maka banyaknya himpunan bagian dari A = 2⁴ = 16
   Yaitu { }, {2}, {3}, {1}, {6}, {2,3}, {2,1}, {2,6}, {3,1}, {3,6}, {1,6}, {2, 3, 1}, {2, 3, 6}, {2, 1, 6}, {1, 3, 6}, {2, 3, 1, 6}.
2. B = { 2, 3, 5, 9, 1 }
   n(B) = 5, maka banyaknya himpunan bagian dari A = 2⁵ = 32

D. Operasi Himpunan

1. Irisan dari Dua Himpunan (Interseksi)
   Misalnya,
   A = { Apel, Anggur, Pepaya, Semangka, Melon }
   B = { Pisang, Anggur, Nanas, Mangga }
   Dalam Diagram Venn digambarkan sebagai berikut :
   
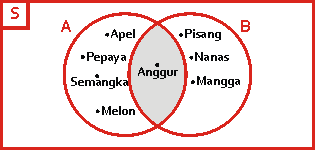
   maka Irisan dari dua himpunan di atas adalah A ∩ B = { Anggur }
2. Gabungan dari Dua Himpunan (Union)
   Gabungan dari dua himpunan ditulis A ∪ B diartikan sebagai himpunan semua anggota A dan B.
   Misalnya,
   A = { 5, 1, 3, 4, 2 }
   B = { 3, 5, 4, 7, 6 }
   Maka A ∪ B = { 1, 2, 3, 4, 5, 6, 7 }
3. Selisih dari Dua Himpunan (Difference)
   Misalnya himpunan A dan B, maka selisih himpunan nya adalah semua anggota A yang bukan anggota B.
   Contoh :
   A = { 2, 3, 6, 8, 9, 4, 5 }
   B = { 3, 5, 2, 6, 1 }
   maka selisih himpunan nya adalah A - B = { 2, 3, 6, 8, 9, 4, 5 } - { 3, 5, 2, 6, 1 } = { 4, 8, 9 } 
4. Komplemen Suatu Himpunan
   Himpunan yang anggotanya bukan anggota A tetapi anggota S (Semesta) maka dinamakan komplemen himpunan A, ditulis A^c atau A'.
   Misalnya,
   A = { 2, 3, 5 }
   Himpunan Semesta (S) = { 1, 2, 3, 4, 5 }
   maka komplemen himpunan A adalah anggota S yang tidak ada di A.
   A^c = A' = { 1, 4 }
5. Pemecahan Masalah Menggunakan Konsep Himpunan
   Misalnya,
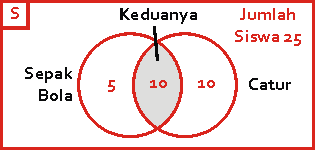
   " Dari 25 Siswa, 15 siswa menyukai olahraga sepak bola, 20 siswa menyukai catur. " tentukan :
   
   1. Siswa yang menyukai sepak bola dan catur
   2. Siswa yang menyukai Sepak bola
   3. Siswa yang menyukai Catur
Jawab :
1. Yang suka keduanya = sepak bola + catur - jumlah siswa = 15 + 20 - 25 = 10
   kalau pakai rumus :
   n(A ∩ B) = n(A) + n(B) - n(A ∪ B)
   n(A ∩ B) = 15 + 20 - 25
   n(A ∩ B) = 10 Siswa menyukai keduanya.
2. Yang suka sepak bola = sepak bola - yang suka keduanya = 15 - 10 = 5 siswa
3. Yang suka catur = catur - yang suka keduanya = 20 - 10 = 10 siswa
Dalam Diagram Venn digambarkan sebagai berikut :

Posted by Adam Prasetya