Persamaan dan Pertidaksamaan Linier

Bahan Stempel Harga Murah, Jelas, Lengkap, Recommended di walisongo.co.id

A. Pendahuluan

Persamaan adalah keadaan dimana suatu pernyataan memiliki kesamaan atau yang serupa dengan yang lain. misalnya 1 + 1 = 3 - 1 ketika di jumlahkan maka hasil nya 2 = 2. berarti 1 + 1 dengan 3 - 1 adalah pernyataan yang sama.

Pertidaksamaan adalah keadaan yang berlawanan dengan persamaan atau pernyataan yang tidak serupa. misalnya 1 + 1 tidak sama dengan 1 - 1, karena 1 + 1 = 2 dan 1 - 1 = 0. jadi 1 + 1 ≠ 1 - 1.

B. Pernyataan dan Kalimat Terbuka

Pernyataan adalah kalimat yang memiliki nilai benar atau salah.

Kalimat Terbuka adalah kalimat yang memiliki nilai kebenaran yang belum jelas.

Contoh Pernyataan :

1. Jakarta adalah Ibukota Indonesia  → Benar.
2. 5 - 1 = 3 → Salah, karena 5 - 1 = 4.

Contoh Kalimat Terbuka :

1. Dia adalah Gurunya → Belum jelas "dia" siapa.
2. x + 7 = -2 → Belum jelas bilangan x nya. 

C. Persamaan Linier Satu Variabel

Persamaan linier satu variabel adalah persamaan yang memiliki peubah (variabel) berpangkat satu dan di tandai dengan tanda "=" atau sama dengan.

Contoh :

1. x + 2 = 10 → variabelnya hanya x
   Maka x = 8
2. 5y + 2 = 12 → variabelnya hanya y
   Maka 5(2) + 2 = 12, y = 2

D. Pertidaksamaan Linier Satu Variabel

Pertidaksamaan linier satu variabel biasanya memiliki tanda

1. kurang dari (<)
2. lebih dari (>)
3. lebih kecil atau sama dengan (≤)
4. lebih besar atau sama dengan (≥)

Contoh :

1. 2x > 5
   Artinya, 2 di kali berapa agar lebih besar dari 5.
   misalnya x = 2 → 2(2) > 5 → 4 > 5 → salah, karena 4 bukan lebih besar dari 5
   Jadi, nilai yang memenuhi x adalah angka yang lebih dari 3.
   x > 3
2. 6x - 5 > x - 10
   ⇔ 6x - 5 + 5 > x - 10 + 5 (ditambah 5)
   ⇔ 6x > x - 5
   ⇔ 6x - x > x - x - 5 (dikurangi x)
   ⇔ 5x > -5
   ⇔ 5x > -5 (dibagi 5)
   ⇔ x > -1
   Jadi, x > -1 adalah penyelesaian dari  6x - 5 > x - 10.
   kita buktikan dulu !
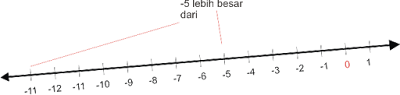
   substitusikan x dengan angka yang lebih dari -1, berarti angka 0.
   6(0) - 5 > 0 - 10
   - 5 > -11 → -5 lebih besar dari -10
   

E. Persamaan Linier Dua Variabel

Bentuk Umum : ax + by = c, misalnya : 2x + 3y = 8 

Kita bisa menyelesaikan persamaan linier dua variabel dengan cara subtitusi dan eliminasi.

Contoh :

1. Subtitusi:
   
   Tentukan himpunan penyelesaian dari :
   x + y = 12 ..... (persamaan 1)
   2x - y = 18 .... (persamaan 2)
   
   Jawab :
   x + y = 12 → x = 12 - y
   subtitusikan x persamaan 2 dengan 12 - y
   
   2(12 - y) - y = 18
   24 - 2y - y = 18
   -2y - y = 18 - 24
   -3y = -6
   y = -6/-3 = 2
   
   substitusikan y di persamaan 1 dengan angka 2
   
   x + y = 12
   x + 2 = 12
   
   maka x = 10
   
   jadi, himpunan penyelesaianya (x, y) adalah (10, 2)
2. Eliminasi:
   
   Ani membeli 2 buku dan 1 pensil dengan harga 12.000. Bento membeli 1 buku dan 3 pensil dengan harga 11.000. Jika Bella ingin membeli 1 buku dan 1 pensil, berapa jumlah uang yang di bayarkan Bella ?
   
   Jawab :
   
   Buku kita lambangkan x
   Pensil kita lambangkan y
   
   Ani → 2x + 3y = 13.000 .... (persamaan 1)
   Bento → 3x + 5y = 20.000 .... (persamaan 2)
   
   2x + 3y = 13.000 | dikalikan 3 → | 6x + 9y = 39.000
   3x + 5y = 20.000 | dikalikan 2 → | 6x + 10y = 40.000
   
   6x + 9y = 39.000
   6x + 10y = 40.000 - (dikurangi)
   0x + (-1y) = -1.000
   
   maka y = -1000/-1 = 1.000
   
   jadi, y = 1.000, y adalah pensil. jadi harga 1 pensil 1.000
   
   kita substitusikan harga 1 pensil dengan salah satu persamaan.
   
   2x + 3y = 13.000
   2x + 3(1000) = 13.000
   2x + 3.000 = 13.000
   2x = 13.000 - 3.000
   2x = 10.000
   x = 10.000/2 = 5.000
   
   maka didapatkan x = 5.000, dan y = 1.000. 1 buku harganya 5.000 dan 1 pensil harganya 1.000
   
   jika Bella ingin membeli 1 buku dan 1 pensil di harus mengeluarkan uang sebesar Rp. 6.000.
   
   
   

Posted by Adam Prasetya