Logaritma

Bahan Stempel Harga Murah, Jelas, Lengkap, Recommended di walisongo.co.id

A. Pengertian Logaritma

Logaritma adalah kebelikan (invers) dari perpangkatan (eksponen)

Fungsi Logaritma dengan bilangan pokok atau basis a dapat dinyatakan sebagai berikut :

F:x  → ^alog x atau y = f(x) = ^alog x

^alog x dibaca "logaritma x dengan bilangan pokok a" Jika ^alog b = c maka b = a^c

• a disebut bilangan pokok, syarat : a > 0 dan a ≠ 1
• b disebut bilangan yang di logaritmakan (numerator), syarat b > 0

B. Fungsi Logaritma

Sifat - sifat logaritma :

• Untuk 0 < a < 1, jika x₂ > x₁ maka log_a x₂ < log_a x₁ atau sebaliknya.
• Untuk a > 1, jika x₂ > x₁ maka log_a x₂ > log_a x₁ atau sebaliknya.

C. Sifat - Sifat Logaritma

Untuk y > 0, a > 0, a ≠ 1, berlaku :

1. ^alog a^c = c ⇒ ^alog a = 1
2. ^alog xⁿ = n ^alog x
3. ^alog x + ^alog y = ^alog xy
4. ^ylog x =  ^alog x / ^alog y = 1 / ^xlog y
5. ^xnlog y = 1 / n ^alog y
6. X^{alog y} = y
7. ^alog 1 = ^alog a⁰ = 0
8. ^alog x = ^anlog xⁿ
9. ^alog x - ^alog y = ^alog x / y
10. ^alog 1 / x = - ^alog x
11. ^alog b . ^blog c . ^clog d = ^alog d

D. Persamaan Logaritma

Persamaan dengan basis memuat variabel yang belum diketahui nilainya adalah persamaan logaritma

Contoh :

log₃ (x + 2) = 9

Himpunan Penyelesaian dari persamaan logaritma berikut untuk a > 0, a ≠ 0, h(x) > 0, h(x) ≠ 0 berlaku sebagai berikut.

• Jika p > 0 dan log_a f(x) = log_a p, diperoleh f(x) = p asalkan f(x) > 0
• Jika log_a f(x) = log_a g(x), diperoleh f(x) = g(x)  asalkan f(x) > 0, g(x) > 0
• Jika log_h(x) f(x) = log_h(x) g(x), diperoleh f(x) = g(x) asalkan f(x) > 0, g(x) > 0
• Jika A{log_a f(x)}² + B{log_a f(x))} + C = 0, diperoleh penyelesaian dengan mengubah menjadi persamaan kuadrat.

E. Penyelesaian Logaritma

Teknik umum penyelesaian logaritma adalah sebagai berikut :

1. Bentuk Umum
   
   ^alog f(x) = k, penyelesaian ⇒ f(x) = a^k dengan f(x) > 0
2. Persamaan Logaritma
   Bilangan pokok disamakan
   
   
3. Bentuk : a ^plog² x + b log x + c = 0
   Penyelesaian :
   persamaan dimisalkan ^plog x = y, kemudian persamaan diselesaikan dengan difaktorkan
   
   a ^plog² x + b ^plog x + c = 0
   
   Penyelesaian ⇒ x₁ . x₂ = p^{- b / a}
4. Pertidaksamaan Logaritma
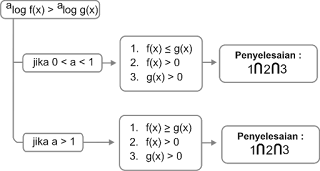
   Langkah pertama adalah samakan bilangan pokok, selanjutnya ikuti aturan dibawah ini!
   

Posted by Adam Prasetya