A. Rumus Umum
Bentuk umum fungsi kuadrat adalah : y = f(x) = ax2 + bx + cRumus Dikiriminan (D) : D = b2 - 4ac
Sumbu Simetri : x = - b 2a
Nila/harga Ekstrim : y = - D 4a atau y = f(- b 2a)
- Terbuka ke atas :
- Terbuka ke bawah :
Titik Ekstrim/ Puncak :
( - b 2a, - D 4a ) atau ( - b 2a, f( - b 2a))
B. Sifat Grafik
Parabola dan sumbu x
D > 0 Parabola memotong sumbu x
D > 0 Parabola memotong sumbu x
D = 0 Parabola menyinggung sumbu x
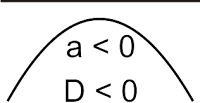
D < 0 Parabola tidak memotong dan tidak menyinggung sumbu x
sehingga :
Parabola dan Garis

| - selalu positif - definit positif - di atas sumbu x - f(x) > 0 | |||
| - selalu negatif - definit negatif - di bawah sumbu x - f(x) < 0 |
Parabola dan Garis

Keterangan :
Diketahui parabola y = ax2 + bx + c dan garis lurus y = mx + c. Jika kedua persamaan di atas disubtitusikan maka diperoleh :
ax2 + bx + c = mx + c atau ax2 + (b - m)x + (c - n)
Bentuk diatas merupakan persamaan kuadrat dimana hubungan sifat antara kedua kurva tersebut dapat ditentukan berdasarkan diskriminannya (D) nya.
⇔ Jika D > 0 → x1 ≠ x2 maka kedua kurva saling berpotongan pada kedua titik.
⇔ Jika D = 0 → x1 ≠ x2 maka kedua kurva saling bersinggungan.
⇔ Jika D < 0 → x1 ≠ x2 maka kedua kurva tidak berpotongan.
C. Menentukan Fungsi Kuadrat
- Memotong sumbu X di x1 dan x2 dan sebuah titik lain.
Gunakan Rumus :y = a(x - x1) (x - x2) - Jika diketahui titik ekstrem (p, q) dan sebuah titik lain.
Gunakan Rumus :y = a(x - p)2 + q - Jika diketahui tiga buah titik sembarang.
Gunakan Rumus :y = ax2 + bx + c


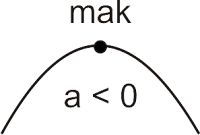





0 Response to "Fungsi Kuadrat"
Post a Comment